Clasificación de los triángulos según la amplitud de sus ángulos.
Acutángulo: Triángulo acutángulo: cuando sus tres ángulos interiores son menores de 90°. El triángulo equilátero es un caso particular de triángulo acutángulo.
Triángulo obtusángulo : si uno de sus ángulos interiores es obtuso (mayor de 90°); los otros dos son agudos (menores de 90°).
Triángulo rectángulo: si tiene un ángulo interior recto (90°). A los dos lados que conforman el ángulo recto se les denomina catetos y al otro lado hipotenusa.
Clasificación de los triángulos según el tamaño de sus lados:
Triángulo equilátero: si sus tres lados tienen la misma longitud (los tres ángulos internos miden 60 grados ó
Triángulo isósceles: si tiene dos lados de la misma longitud. Los ángulos que se oponen a estos lados tienen la misma medida. ( Tales de Mileto, filósofo griego, demostró que un triángulo isósceles tiene dos ángulos iguales, estableciendo así una relación entre longitudes y ángulos; a lados iguales, ángulos iguales).
Triángulo escaleno: si todos sus lados tienen longitudes diferentes (en un triángulo escaleno no hay dos ángulos que tengan la misma medida).
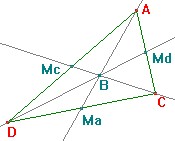
Rectas y puntos notables de un triángulo:
Altura: Se llama altura de un triángulo a cada una de las tres rectas que pasan por un vértice del triángulo y que son perpendiculares al lado opuesto del vértice. La intersección de la altura y el lado opuesto se denomina pie de la altura y estos puntos se cortan en un punto único llamado el ortocentro.
Mediana: son las tres rectas que unen cada vértice del triángulo con el centro del lado opuesto. En el ejemplo, son (AA'), (BB') y (CC'), Las tres medianas se cortan en un único punto llamado centro de gravedad o centro de masa del triángulo.
Mediatriz: cada una de las mediatrices de sus lados [AB], [AC] y [BC], Las tres mediatrices de un triángulo son concurrentes en un punto O equidistante de los tres vértices. La circunferencia de centro O y radio OA que pasa por cada uno de los tres vértices del triángulo es la circunferencia circunscrita al triángulo, y su centro se denomina circuncentro.
Bisectriz: son los ángulos internos de un triángulo en los cuales se forma la llamada bisectriz que vienen siendo en forma de rectas a partir de cada angulo que se interceptan, las tres bisectrices de un triángulo son concurrentes en un punto O.
Ortocentro: Se denomina ortocentro (símbolo H) al punto donde se cortan las tres alturas de un triángulo. Tres rectas cualquiera, tomadas a pares, podrían intersectarse en tres puntos diferentes, pero en el caso de las alturas de un triángulo dado, puede demostrarse que se intersectan en un solo punto, es decir, en el ortocentro, El ortocentro se encuentra dentro del triángulo si éste es acutángulo, coincide con el vértice del ángulo recto si es rectángulo, y se halla fuera del triángulo si es obtusángulo.
Baricentro: es uno de los puntos característicos de un triángulo y es el punto de intersección de las medianas de cada uno de los lados.
Circuncentro: (símbolo O) es el punto en el que se intersectan las tres mediatrices de un triángulo y es el centro de la circunferencia circunscrita.
Incentro: (símbolo I) es el punto en el que se intersectan las tres bisectrices de los ángulos internos del triángulo, y es el centro de la circunferencia inscrita en el triángulo y que equidista de sus tres lados, siendo tangente a dichos lados.
Análisis del video Nature by Numbers
A) Pude identificar luego de la investigación anteriormente realizada que se forma una mediatriz luego de que se crean los giraloses en el video, se van creando punto por punto y se ven 2 rectas a las cuales con su unión se les encuentra la mediatriz y de pronto se crea un tercer punto de el cual salen mas mediatrices las cuales se intersectan con la primera y se forma la misma demostración varias veces.
B) Realmente es impresionante el video, se va notado poco a poco como todo va cambiando y es aun mejor cuando uno lee el hecho de cómo todo tiene la lógica de porque cambia a su siguiente forma por un sentido o por alguna operación matemática o mejor dicho que todo esta relacionado con figuras que se encuentran en las matemáticas y me llamo mucho la atención que la naturaleza prácticamente es matemática sin quererlo es decir cada pequeña figura, cada cosa nos demuestra que tiene que ver con algo, me encanto el hecho que comienza con números y operaciones matemáticas y que a partir de eso se crea todo los demás.
Links:
http://es.wikipedia.org/wiki/Tri%C3%A1ngulo_acut%C3%A1ngulo#Mediatrices_y_circunferencia_circunscrita []
















Buena investigación. Aprobada la actividad.
ResponderEliminar