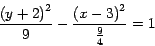Calculo 1: noviembre 2010

La hipérbola:

Definición: Es el lugar geométrico de puntos, cuya diferencia de distancia a dos puntos (focos) es constante e igual a: 2a

| d(P,F) - d(P,l) |=2a

Elementos de la hipérbola:

Focos: Son los puntos fijos F y F'.

Eje focal: Es la recta que pasa por los focos.

Eje secundario o imaginario: Es la mediatriz del segmento .

Centro: Es el punto de intersección de los ejes.

Vértices: Los puntos A y A' son los puntos de intersección de la hipérbola con el eje focal.

Los puntos B y B' se obtienen como intersección del eje imaginario con la circunferencia que tiene por centro uno de los focos y de radio c.

Radios vectores: Son los segmentos que van desde un punto de la hipérbola a los focos: PF y PF'.

Distancia focal: Es el segmento de longitud 2c.

Eje mayor: Es el segmento de longitud 2a.

Eje menor: Es el segmento de longitud 2b.

Ejes de simetría: Son las rectas que contienen al eje real o al eje imaginario.

Asíntotas: Son las rectas de ecuaciones

Las asíntotas de la hipérbola se muestran como líneas discontinuas azules que se cortan en el centro de la hipérbola (curvas rojas), C. Los dos puntos focales se denominan F₁ y F₂, la línea negra que los une es el eje transversal. La delgada línea perpendicular en negro que pasa por el centro es el eje conjugado. Las dos líneas gruesas en negro paralelas al eje conjugado (por lo tanto, perpendicular al eje transversal) son las dos directrices, D₁ y D₂. La excentricidad e (e>1), es igual al cociente entre las distancias (en verde) desde un punto P de la hipérbola a uno de los focos y su correspondiente directriz. Los dos vértices se encuentran en el eje transversal a una distancia ±a con respecto al centro.

Excentricidad
La excentricidad mide la abertura mayor o menor de las ramas de la hipérbola.

Ecuación reducida de la hipérbola

Si el eje real está en el eje de abscisas las coordenadas de los focos son:

F'(-c, 0) y F(c, 0)

Ecuación de la hipérbola con los focos en el eje OY

Si el eje real está en el eje de abscisas las coordenadas de los focos son:

F'(0, -c) y F (0, c)

Ecuación de la hipérbola con eje paralelo a OX, y centro distinto al origen

Si el centro de la hipérbola es C(x₀, y₀) y el eje principal es paralelo a OX, los focos tienen de coordenadas F(X₀+c, y₀) y F'(X₀-c, y₀). Y la ecuación de la hipérbola será

Al quitar denominadores y desarrollar las ecuaciones se obtiene, en general, una ecuación general:

Donde A y B tienen signos opuestos.

Ecuación de la hipérbola con eje paralelo a OY, y centro distinto al origen

Si el centro de la hipérbola C(x₀, y₀) y el eje principal es paralelo a OY, los focos tienen de coordenadas F(X₀, y₀+c) y F'(X₀, y₀-c). Y la ecuación de la hipérbola será:

Al quitar denominadores y desarrollar las ecuaciones se obtiene, en general, una ecuación general:

Donde A y B tienen signos opuestos.

Ecuación de la hipérbola equilátera

Las hipérbolas en las que los semiejes son iguales se llaman equiláteras, por tanto a = b. Y su ecuación es:

Las asíntotas tienen por ecuación:

y=x, y=-x

Es decir, las bisectrices de los cuadrantes.

La excentricidad es

Ecuación de la hipérbole equilátera referida a sus asíntotas

Para pasar de los ejes OX, OY a los determinados por las asíntotas, bastará dar un giro de -45° alrededor del origen de coordenadas. Quedando la ecuación como:

Si efectuamos un giro de 45° en los ejes, la hipérbola que queda en el segundo y cuarto cuadrante y su ecuación será:

Ejemplo:

Hallar la ecuación canónica de la hipérbola con vértices en (3,-5)y (3,1)y asíntotas y = 2x-8y y = -2x+4. Además calcule los focos, la excentricidad y trace la gráfica.

Solución
Por ser el centro el punto medio de los vértices sus coordenadas son (3, -2). Además, la hipérbola tiene eje transversal vertical y a=3. Por otro lado, por el teorema de las asíntotas.