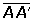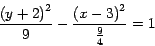Nombre | Enunciado (La regla de derivación expresada en palabras) | Función(Es una generalización) | Función derivada | Ejemplo | ||
Función | Derivada | Planificación y argumentación | ||||
Derivada de una constante | La derivada de una constante es cero. | y = k | y’ = 0 | y=ln(2) | y’ =0 | Analizo la función, observo que es un número real, no depende de ninguna variable, por lo tanto su derivada es cero. |
Derivada de una potencia (exponente un número real) | La derivada de una función con exponente de un número entero, es igual al producto de el exponente y la variable, elecado al exponente inicial menos 1. | Y=xn | y’ = n xn-1 | Y= x^6 | Y’=6x^5 | Se debe modificar y bajar el exponente de tal manera que éste multiplique a la variable respecto a la cual estamos derivando, luego al mismo exponente se le resta la unidad (n). |
Derivada de una constante por una función | La derivada de una constante por una función es la misma constante por la derivada de la función. | y=k f(x) | Y’= k f’(x) | Y= 6x^4 | Y’=6.4x^3 Y’=24x^3 | Estudio las características de la función, si es el producto de una constante por una función, derivo la función y la multiplico por la misma constante. |
Derivada de una suma de funciones | La derivada de una suma (o diferencia ) de funciones es la suma (o la diferencia) de las derivadas | Y= f(x)+/-g(x) | Y’= f’(x)+/-g’(x) | y = 3+2x^5 | y’=0+10x^4 y’= 10x^4 | Primero se determinan las derivadas de las funciones por separado, y luego se suman para luego lograr de resultado la derivada. |
Derivada de un producto de funciones | La derivada de una producto de funciones es la derivada de la primera función por la segunda sin derivar, más la derivada de la segunda función por la primera sin derivar | Y=f(x).g(x) | Y’=f’(x)g(x)+f(x)g’(x) | Y’=(x^2+5)(x^3) | Y’=(x^2+5)’(x^3)+(x^2+5)(x^3)’ Y’=(2x)(x^3)+(x^2+5)(3x) Y’=2x^4+3x^3+15x | Se coloca la derivada de la primera por la segunda original, sumando a la primera original por la derivada de la segunda. Se resuelve la derivación. |
Derivada de un cociente de funciones | La derivada de un cociente de funciones es un fracción que tiene por numerador la derivada del númerador por el denominador sin derivar, menos la derivada del denominador por el numerador sin derivar, todo dividido entre el denominador original al cuadrado | Y= f(x) g(x) | Y’=f’(x).g(x) -f(x)g’(x)/g(x) | h(x) = 3x+1 2x | h’(x)= (3)(2x)-(3x+1)(2) (2x) ^2 h'(x)= 6x-6x+2 4x ^2 h'(x)= 1 2x ^2 | Se identifica la función que esta en el numerador y la que esta en el denominador. Se escribe la derivada del numerador por el denominador y se le resta el numerador por la derivada del denominador, y se divide todo entre el denominador elevado al cuadrado. |
Derivada de logaritmo neperiano | La derivada de la función de logaritmo neperiano se obtiene al dividir la derivada de la función entre la función inicial sin derivar. | Y= ln(x) Y=ln(u) | Y’= 1 X Y’= u’ u | f(x)= ln( 2x^4-x^3+3x^2-3x) | f’(x)= 8x^3-3x^2+6x-3 2x^4-x^3+3x^2-3 | Se identifica que tipo de logaritmo es. Si la función es el logaritmo neperiano de x, para derivar se coloca uno entre x. Y si es el logaritmo neperiano de una función se derivada la función y se divide entre la misma función sin derivar. |
Derivada de exponencial | La derivada de la función exponencial es igual a la misma función por el logaritmo neperiano de la base y por la derivada del exponente. La derivada de la función exponencial de base e es igual a la misma función por la derivada del exponente. | Y=e^x Y= a^x Y=a^u | Y’=e^x Y’=a^x.lna Y’=u’.a^u.lna | f(x)= 3^x f(x) =2^(x^2)-1 | f’(x)=3^x.ln3 f’(x)=2x. 2x^2-1.ln2 | Se estudia que tipo de función, pueden existir varios tipos, es a^x se coloca la misma expresión multiplicando al logaritmo neperiano (Lne) de la base, Si es ex la derivada es la misma expresión, Si es del tipo a^u, se escribe la derivada del exponente por la expresión original por el logaritmo neperiano de la base. |
Función trigonométrica | Derivada |
y=cos (x) y=sen(x) y=tg(x) y=ctg(x) y=sec(x) y=csc(x) | Y’=-sen x Y’=cos x Y’=sec^2 x Y’=-csc^2 x Y’=sec x .tan x Y’=-csc x .cot x |
· Antes de aplicar una regla de derivación, ¿qué debes hacer, independientemente de cuál sea la función?
Debes verla y considerar que derivada es y si lo es que clase de reglas puedes aplicar en ella para resolverla.
· ¿Se puede aplicar la misma regla a todas las funciones? ¿Por qué?
No, puesto que existen varios pasos a seguir para poder resolver estos ejercicios y se deben de cumplir cada una de estas reglas para lograr obtener un resultado bueno.
· ¿Se puede derivar una misma función utilizando reglas diferentes?. ¿Por qué?
Si se puede porque de acuerdo a las matemáticas se pueden utilizar varios tipos de estas reglas mencionadas para resolver estas operaciones pero claro siempre con el uso indicado de las reglas.
2) Estrategia para derivar funciones:
¿Que tipo de función es?
¿Que tipo de regla(s) de derivación puedo utilizar para resolverla?
Resuelvo la operación según las leyes establecidas
¿Se podría simplificar mas esta respuesta?... de no poder hacerlo mi ejercicio estaría completo, de poder hacerlo es que todavía me faltan pasos para completar mi ejercicio.